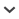Introduction

Lichenometry has principally been used to date periglacial and glacial landforms. Since the pioneering work of Beschel (1961), this technique has been applied to a large variety of environments. It is especially well suited for arctic and alpine regions because other dating methods are either difficult to implement or even fail at these high altitudes. For example, the sparsity of vegetation near glaciers makes the use of dendrochronology problematic. Although lichenometry may be used to date old surfaces (e.g. the late Holocene in South America; Rodbell, 1992), it is best suited to analyze recent centuries for which classical ¹⁴C dating techniques are tainted with a low precision.

The basic premise of lichenometry is that the diameter of the largest thalli growing on a surface is proportional to the length of time that the surface has been exposed to colonization and growth in a specific environmental context. Hence, if one can establish a temporal link between lichen sizes and their ages, i.e. construct a growth curve, it is then possible to date moraines. However, this relationship between the lichen size and its age varies with the characteristics of the surroundings. Lichen growth depends on the climate (Benedict, 1967, 1990, 1991), the lithology (Rodbell, 1992), as well as the orientation of the colonized surface (Pentecost, 1979). The most popular approach that involves measurements of the largest lichens is assuming that the largest individual lichens are among the first to colonize a surface. Although there is a common agreement among geomorphologists about the basic concepts of this method, there is still controversy concerning its implementation, e.g. the number of lichens sampled, the design of the experiment, and the choice of a robust statistic.

Recently, McCarroll (1994) proposed a new strategy where only the largest lichen on a block is selected. This procedure is then repeated many times on different blocks. However, McCarroll incorrectly assumed that the largest lichen sizes are near normally distributed (see figures 2 and 7 in McCarroll, 1994). This assumption was only based on a visual inspection of histograms, and neither statistical tests were provided to confirm this choice nor mathematical concepts employed to justify this approach. The latter point is important because probability theory dedicated to extreme values (largest lichen diameters belonging to this category) dictates that the distribution of maxima cannot be normal (Fig. 1) but instead must follow a specific distribution (the Generalized Extreme Value distribution), whenever the sample size is large enough. This mathematical result has been used in many fields since the pioneering work of Gnedenko (1943) but has rarely been applied to lichenometry (e.g. Bull and Brandon, 1998; Karlen and Black, 2002). (A detailed description of this theory, as well as a list of references, will be given in the section MODELING MAXIMUM DIAMETERS.) An immediate consequence of this mathematical constraint is that past computations of confidence intervals based on the assumption of normality are at best questionable and at worst flawed. To illustrate the importance of the appropriate choice for the distribution of maxima, we plot in Figure 1 the histogram of the maximum lichen diameters from the Charquini glacier in Bolivia (the same result has been obtained for different moraines and regions). From the histogram shapes, it is very clear that the distributions of maxima are rarely symmetric, and the fit by a Gaussian density distribution (dotted line) is too restrictive to represent accurately maximum lichen sizes (e.g. Fig. 1a). In comparison, the fit by a Generalized Extreme Value (GEV) density distribution (solid line) that is presented in detail in MODELING MAXIMUM DIAMETERS provides a much better agreement with the data, because the GEV spans a much wider range of distribution shape and it is specially adapted to deal with maxima. In the past, other authors have noticed this discrepancy between the maximum distribution and a Gaussian fit. Bull and Brandon (1998) and Karlen and Black (2002) made use of the Gumbel distribution to model the maximum diameters density, but these authors did not take full advantage of the extreme value theory. The Gumbel density is only a special case of the GEV density which is a larger class of distribution (see MODELING MAXIMUM DIAMETERS). In addition, no statistical model based on the Gumbel distribution was implemented to derive estimation errors and confidence intervals. A few past studies (e.g. O'Neal and Schoenenberger, 2003) attempted to associate confidence intervals and/or p-values with specific growth curves. However, the hypothesis to derive these confidence intervals, when implementing linear or nonlinear regression models, was formulated as: maximum diameter = l(age) + noise, where l is the growth curve and the noise Gaussian. This last assumption, as seen in Figure 1, is not satisfied.

Figure 1

Distribution of maxima lichen diameters (mm) on six moraines of the Charquini south glacier. The black boxes corresponds to the histogram of the data. The dotted line shows the fit by a Gaussian density distribution. The solid line indicates the fit by a Generalized Extreme Value (GEV) density distribution. The number of lichen per panel is about 20.

One of our main goals in this paper is to introduce a sound statistical model based on extreme value theory, which is more appropriate to model the distribution of the raw material of lichenometry: the largest lichen diameters.

This paper is organized as follows. In the next section, a model specifically tailored for analyzing maxima and based on the statistical extreme values theory is presented. A full description of the field site (Cordillera Real, Bolivia) can be found in the section AREA OF INTEREST. The observation collection process is detailed in the section FIELD WORK. This field study is a part of a larger French program (Great Ice) dedicated to the study of climate and environmental variability in the Andes and during the Little Ice Age (Solomina et al., 2007). To our knowledge, no previous lichenometry studies have been undertaken in Bolivia, and consequently there is no growth curve for this region. The section Conclusions and Future Work summarizes our results.

A General Statistical Model For Lichen Diameters Analysis

To develop a statistical model for analyzing lichen diameters, we first need to identify the main sources of randomness. In our approach, we focus on two main sources of uncertainty: the error in modeling lichen diameters, and the error of associating a date with a moraine. Consequently, we model a bivariate random vector, say (X_i, T_i), the date of the i-th moraine T_i and the lichen diameters associated to this moraine X_i, where the moraine index i varies from 1 to m, the total number of moraines. With these notations, X_i = {X_i,1, …, X_i,ni} is a vector whose length n_i corresponds to the number of sampled blocks on the i-th moraine. Apart from a few cases for which the date of the moraine is known, the variable T_i is not observed and has to be estimated from the lichen diameters. Deriving this date is one of the most important questions in the analysis of lichen diameters. To solve this problem, we propose a statistical model that has the advantage of being global, i.e. the lichen information (the measured diameters and the moraine dates when available) is pooled into one data set. In past studies, two distinct data sets were considered; lichens with known dates were analyzed separately from lichens with unknown dates (e.g. McCarroll, 1994). Then, these two groups were linked by the growth curve. We argue that all parameters describing the temporal evolution of lichen diameters should be estimated simultaneously. The two main reasons for such a position are the following: (1) Separating the lichens into two groups is statistically arbitrary because it is typically assumed that the distribution of lichen diameters comes from the same family of distribution (otherwise it would not be possible to make inference from dated moraines to undated ones). (2) Past two-step procedures have the disadvantage of propagating the error generated from the first step into the second stage of the estimation of dates. In comparison, a global pooling of all data allows us to maximize a global criteria to estimate the parameters of our statistical model, and consequently it reduces the estimation error.

Another difference with past studies is that the dates T_i are not necessarily considered as real numbers but are viewed as random variables, i.e. realizations from a common distribution function. This approach allows us to measure the second source of uncertainty, the error in dating the lichens. For example, carbon dating does not provide a unique date but instead proposes a range of values for the moraine date. To the best of our knowledge, the integration of these two uncertainties into a global framework is novel in most lichenometry studies. Note that capital letters (e.g., X and T) are used to denote random variables, and lowercase letters (e.g., x and t) correspond to realizations, i.e. specific outputs for the random variables.

Modeling Maximum Diameters

Extreme value theory has been applied to a variety of problems in finance (Embrechts et al., 1997), hydrology (Katz et al, 2002), and ecology (Gaines and Denny, 1993). In recent years, the statistical methodology for extremes has also been used for a wide range of problems in climate studies. Extreme climate events due to their large economic and human impacts are becoming more and more studied in geophysics. For example, Kharin and Zwiers (2000) examined changes in climate extremes from coupled atmosphere-ocean GCM outputs, while Naveau and Moncrieff (2003) investigated the role of extremes on upward mass fluxes. To learn more about extreme value theory, the book by Leadbetter et al. (1983) is recommended. For more recent and applied work, we refer to Coles (2001), Smith (1992), Naveau et al. (2005), and Reiss (1997). But what is exactly extreme value theory? Its basic principles come from an asymptotic probabilistic result. The original focus of the theory was to describe the behavior of maxima when the sample size became larger and larger. To better understand this approach, we will first recall in the next paragraph a classical asymptotic result for the sample mean and then we will describe what happens for the sample maxima.

Most statistical inference methods are concerned with the center of a probability distribution (mean) and the deviation from it (variance). One reason for the popularity of such methods is that the assumed distribution is Gaussian, which is uniquely characterized by its mean and its variance. This assumption is justified by a famous theorem in probability, the Central Limit Theorem (CLT), which states the distribution of the sample mean is approximately Gaussian for large samples (whenever the variance is assumed to be finite). The advantage of assuming a Gaussian distribution for the sample mean is that confidence intervals can be then easily derived. Unfortunately, the sample maximum rather than the sample mean has been the primary variable of interest in many recent lichenometry studies (Solomina et al., 2007; McCarroll, 1994). Hence, the CLT can not be applied to approximate the distribution of the maximum (see Fig. 1).

As an alternative, we use a less-known but nevertheless similar result to the CLT. The difference is that this asymptotic result is specially tailored for maxima, and it can be summarized in the following way. The distribution of the maximum in large random samples is known and follows a specific distribution called the Generalized Extreme Value distribution (GEV). The GEV cumulative distribution function is equal to

1

where μ, σ > 0 and ξ are the location, scale, and shape parameters, respectively. The shape parameter drives the tail behavior of G. For example, the classical Gumbel distribution corresponds to ξ = 0. If ξ > 0 (Fréchet type), then the distribution is heavy tailed, i.e. the right tail of the distribution decreases at a much slower rate than a Gaussian tail, and higher moments like the variance may not be finite. If ξ < 0 (Weibull type), it has a bounded upper tail. For example, the solid lines in Figure 1 correspond to GEV densities with different shape parameters. Hence, the sign and value of the shape parameter is very important when modeling the behavior of the maximum. At this juncture, we stress that the distribution of maximum diameters is not chosen arbitrarily; rather the GEV is the unique distribution derived theoretically for modeling the maxima. It is important to note that the GEV fits maxima not only from a Gaussian sample, but also from all classical continuous distributions (e.g., exponential, uniform, Cauchy, etc.). We refer to the book by Embrechts et al. (1997) for an in-depth discussion about the conditions of this convergence. Hence, this methodology is very general and independent of specific numerical values. Note that the case ξ = 0 in Equation (1) can be viewed as the limiting result: lim G(x; μ, σ, ξ) = G(x; μ, σ, 0) as ξ goes to zero. Hence, in the rest of this paper, we will only present our mathematical derivation for the case ξ ≠ 0; the case ξ = 0 can be obtained by letting ξ go to zero.

In this paper, we denote the maxima as

where X_i,j,k are the n_i,j,k lichen diameters on the jth block from the ith moraine, and m is the number of moraines. We suppose that the lichen diameters on a block are independent and follow the same distribution. Between blocks, the lichens are assumed to be independent but they do not have the same distribution. Although we do not necessarily know the value of n_i,j,k and X_i,j,k, we assume that the maximum X_i,j comes from a sample of lichen diameters whose size is relatively large.

From the aforementioned extreme value theory, i.e. Equation (1), it is logical to assume that the probability density function of the maximum lichen diameter X_i,j follows a GEV density,

2

for all i = 1, …, m and j = 1, …, n_i. Compared to Equation (1) in which the parameters μ, σ, and ξ were fixed, Equation (2) shows that the parameters describing lichen diameter distributions can now vary in time through the index of the moraine i (we suppose that the moraine index i is ordered in time, i = 1 representing the youngest moraine and i = m corresponding to the oldest one). The reason for such a choice stems from the very nature of lichenometry, which studies the temporal evolution of large lichen diameter properties from moraine to moraine. Consequently, the behavior of μ_i, σ_i and/or ξ_i should capture the temporal variation of the lichens. For our case study, which will described later in this paper, Figure 2 displays the variation of the location, log-scale, and shape parameters in function of the moraines' order. This graph clearly shows that the location parameter varies linearly in function of the moraines' ages, while the scale and shape parameters behave more randomly. In the case study, we will describe how such information can be taken into account in a global statistical model.

Figure 2

Exploratory study of the maximum lichen diameters measured on ten moraines of Charquini south glacier in Bolivia. The upper, middle, and lower panels correspond to the log-scale, location, and shape GEV parameters [see Equation (2)] in function of the moraine order, respectively, called μ, log σ, and ξ. The moraine M1 represents the youngest one and moraine M10 the oldest. The vertical dotted lines show the 95% confidence intervals. Note that these intervals are very small for the parameter 1a and that they are missing for moraines M2 and M5 due to numerical instabilities.

Distribution of Lichen Ages

In lichenometry, there are two categories of dated surfaces. The first one is characterized by the presence of a confidence interval. For example a date computed with a ¹⁴C carbon dating procedure is classically associated with lower and upper bounds. For this category, we can assume that T_i follows a Gaussian variable with mean α_i and standard deviation β_i; the latter parameter being inferred by the ¹⁴C carbon dating procedure. In this case, the density of T_i is given by

3

The second category corresponds to the situation in which the estimated moraine date is not associated with any error analysis, for example a date inferred from a historical map or a human-made structure. In this case, we have two options: either we assume that the estimated date of the moraine is perfect, or we arbitrarily choose to fix a small standard deviation β that characterizes the a priori error. For example, even a surface dated from a historical map can be tainted with an error of ±3 years with a confidence of 95% (it is difficult to argue that the age of the moraine can be below this error range). Because we prefer to overestimate rather than underestimate the error for our undated surfaces, we opt for the second solution in this study. In this case, the Gaussian density defined by Equation (3) can be used with β = 3 years/1.96 ~ 1.5.

Linking the Maximum Lichen Diameters and the Moraine Ages

The last step in our construction is to relate the distribution of the maximum lichen diameters with the moraine ages (the dated and the undated ones). We assume that the joint distribution of (X_i,j, T_i) can be written as the product of a GEV and Gaussian distribution, and the parameters of the two distributions are linked through the relationship α_i = l(μ_i) for some growth function l. In other words, we suppose that lichen diameters and moraine ages are independent variables (in distribution) but are linked through their parameters. Equations (1) and (2) yield to the joint density function:

4

and where θ represents the vector of all parameters: θ = [(μ₁, μ₂, …), (σ₁, σ₂, …), …]. The above formula is very general and, depending on the case under study, it can be simplified.

Estimation of Our Model Parameters

The next stage is to describe a procedure for estimating the unknown parameters represented by the vector θ whenever a set of data has been obtained. Suppose that all moraine dates are available. The likelihood function that is defined as the probability of observing our data for a given set of parameters θ is equal to

5

Under the assumption that all t_i's are observable, the optimal parameter vector θ is the one that maximizes l(θ). In practice, we only know the t_i's for the dated surfaces. To fill in the missing dates, we implement the Expectation-Maximization (EM) algorithm, a recursive process for obtaining maximum likelihood estimates with incomplete data (McLachlan and Thriyambakam, 1997; Dempster et al., 1977). On each iteration of the EM algorithm, there are two steps called the E-step (Expectation) and the M-step (Maximization). This algorithm is closely related to the ad hoc approach to estimation with missing data, where the parameters are estimated after filling in initial values for missing values. The latter are then updated by their predicted values using these initial parameters. The parameters are then re-estimated, and so on, proceeding until convergence. The M-step involves only complete-data maximum likelihood estimation, which is computationally simple [see Equation (5)]. The E-step deals with the expectation of the complete-data log likelihood given the observed data (see McLachlan and Thriyambakam, 1997, for more details).

A Case Study: the Charquini Glacier in Bolivia

Area of Interest

The field work was conducted in the Huayna Potosi–Condoriri massifs (Fig. 3) in the Cordillera Real (16°21′S, 68°07′W) on the eastern part of the Andean chain, about 50 km north of La Paz, Bolivia. To complement our data set, isolated observations were also taken in the northern part of Bolivia in the Cordillera Apolobamba. These areas are dominated by summits reaching 5000 to 6100 m a.s.l. (Huayna Potosi, 6088 m a.s.l.) and comprised of massive batholiths (granite) and metamorphic rock (quartzites). The climate in this region is defined by the position of the Intertropical Convergence Zone (ITCZ), the oscillation responsible for a marked rainy seasonal variability in the eastern Andean area (Aceituno, 1988; Ribstein et al., 1995; Vuille at al., 1998; Garreaud, 1999). The southern winter (May to September) produces a dry and cold season generated by the northward displacement of the mid- and upper tropospheric westerlies. The southern summer (November to March) is warm and wet. This area within the ITCZ is characterized by low seasonal variations in solar radiation and temperature and by a marked seasonality in precipitation. Precipitation was measured on the Plataforma Zongo, 2 km from Charquini, where the annual average precipitation from 1971 to 2000 was about 835 mm at 4800 m a.s.l. (Caballero et al., 2002). Around 65% of the rain falls from December to February. Monthly average temperature variations do not present a large amplitude. The 0°C isotherm remains above 4900 m throughout the year. A recent study of the snow cover duration near the glacier studied therein showed that snow represents around 26% of precipitation and that the snow cover at 4900 m during the rainy season stays on the ground rarely more than three days, with a modal value of one day and a maximum of six days (Chevallier, 2002). The Equilibrium Line Altitude of glaciers is between 5200 and 5400 m a.s.l. The periglacial environment is relatively spread in altitude, and permafrost may exist locally from 5400 m a.s.l. (Francou et al., 2001; Ramirez et al., 2001).

Figure 3

The Bolivian region of interest for this study (Cordillera Apolobamda and Cordillera Real). The numbering on this map refers to Table 1.

Table 1

Characteristics of the dated surfaces.

Field Work

Our data set of lichenometric measurements of Rhizocarpon sp. (ex Rhizocarpon geographicum) was divided into two groups: 10 dated surfaces and 10 undated moraines. The latter group constituted the main focus of our investigation, the undated moraines on the Charquini glacier. All measurements on this glacier were made on the external side of lateral moraines on both sides of the valley (see Table 2 for the sampling characteristics). We selected at least 180 blocks per moraine with 90 on either side of the valley. For each block, the single largest lichen was measured. The lichen size ranged from 10 to 50 mm, while the block position with respect to the moraine axis was noted. We were not able to detect any significant spatial variation from block to block.

Table 2

Characteristics of the lichen sampling for the Charquini south glacier.

For the second group, different dating techniques (historical documents, aerial photos, carbon dating, etc.) were employed to derive associated dates. Table 1 summarizes the results of this dating procedure; the fact that the same date could be obtained by different techniques explains the redundancy of a few dates in our table. Geographically, six dated moraines from four glaciers were located in the Huyana Potosi Massif (Charquini, Chacaltaya, Janqu Uyu, and Zongo).The oldest moraine of our sample was carbon dated (¹⁴C from peat samples; see Table 1 and Stuiver at al., 1998).The known spread was included in our statistical analysis by fixing the dating range for this moraine. Otherwise we assumed that the standard deviation β in Equation (3) of all the other dated surfaces in Table 1 was fixed and equal to 1.5 years. In Table 1, there was also a category of surfaces comprised of a variety of human-made structures such as archeological monuments, rock-wall cut, stonewalls during the construction of a road, artificial dams, and irrigation canals. For these diverse surfaces, the sampling was performed in the following way. In the case of rocky slopes, the single largest lichen was selected inside an area of 1 m². This procedure was repeated on 60 different sampled surfaces. In the case of housing walls, measurements were taken on inside walls as well as outside ones, but no difference was identified between them. Similar measurements were performed on the Milluni dam that was constructed from stones of 30–50 cm length along the a-axis. We also tried to take measurements on walls of old buildings like colonial churches but all these trials were unsuccessful. Finally, all measurements were taken with a flexible, transparent plastic rule with an accuracy of 1 mm. The smallest measured diameter was 2 mm. Anomalous lichen shapes were rejected to reduce the risk of coalescence. At the end of this field campaign, around 6800 measurements were obtained, i.e. 4156 for dated surfaces and 2600 on the Charquini glacier.

Statistical Analysis of the Bolivian Data

Exploratory Analysis of the Gev Fit with Respect to the Moraine Order

As a preliminary step before modeling all the elements of the likelihood function defined by Equation (5), it is interesting to have a crude idea of the temporal variation of the three GEV parameters. For each of the 10 moraines found on the Charquini south glacier, the maximum diameter lichen distribution is independently fitted by maximizing the likelihood obtained from Equation (2). Figure 2 displays estimates of the GEV location, shape, and log-scale parameter for each moraine. The vertical dotted lines correspond to the 95% confidence intervals. Each of the three panels is discussed separately in the following paragraphs.

The GEV location parameter μ_i in Equation (2) corresponds to the main temporal trend in maximum lichen diameters. For example, a linear trend should fit adequately our Bolivian data (see the middle panel of Fig. 2). In general, the μ_i's play an equivalent role of the growth curve. After a rapid increase during the earlier part of the lichen life caused by competitive stress, the growth curve follows a roughly linear trend, and finally its value converges to a plateau which reflects the slowing down of the lichen growth. These different phases can be parameterized by a mathematical formula depending on the time period under study. For our Bolivian lichen diameters, the middle panel of Figure 2 clearly shows that our data span the linear period of the lichen growth.

In contrast to the location parameter, the GEV shape parameter ξ_i represents the large-scale behavior of lichen distributions. For our particular case study in Bolivia, there is no reason to think the moraines had been perturbed by large-scale changes in the last few centuries. In addition, the lower panel of Figure 2 clearly shows two features. First, the shape parameter does not display a clear temporal pattern, and second, there is a large variability among our individual estimated shape parameter values. This last issue is due to the statistical difficulty of estimating ξ_i's for small samples, i.e. estimating separately ξ_i for each moraine i. For moraines M2 and M5, it is not even possible to compute confidence intervals due to numerical instabilities in the likelihood estimation procedure of ξ_i. These two reasons justify our main model choice. We assume that ξ_i is a constant for all moraines found on the Charquini south glacier. Of course, if there is geophysical or climate evidence that an abrupt temporal change had occurred for a particular glacier, then this information should be integrated in our model.

The scale parameter σ_i has to obey a mathematical constraint; it must be positive. For this reason, log σ_i is classically parameterized (instead of σ_i). As seen in Figure 2, it may be possible that log σ_i follows a particular trend, but it is very difficult to visually decide if such a possible trend is significant. To solve this issue, we need to introduce a few concepts about model selection.

Model Selection

From Figure 2, we learned that a linear parameterization is reasonable for modeling the location parameter. Hence, our general likelihood function defined by Equation (5) can be simplified as

6

where the β_i's are given by Calib 4.4 (Stuiver et al., 1998) from ¹⁴C carbon dates.

To completely define our likelihood function, we still need to propose a parameterization for the log-scale parameter log σ_i in Equation (6). In Table 3, we propose and compare three different models for the log-scale parameter. The simplest one corresponds to a linear model for log σ and for the most complex, we suppose a different log σ for each moraine. As an intermediate step, we also investigate a quadratic trend. An important issue related to the choice of the appropriate model with respect to our data is the problem of over-parameterization, fitting the data very well but with a large number of parameters. For example, 10 data points can be perfectly modeled by 10 parameters but the predictive value of such an over-parameterized model is null. To compare the models described by the first two columns of Table 3, we compute the Akaike Information Criterion (AIC) (George, 2000) that is defined by AIC = −2 log l(θ) + 2k, where k is the number of parameters in our model (see Table 3). Heuristically, one can view the first term, −2 log l(θ), as a measure of lack of fit, while the second term, 2k, can be interpreted as a “penalty” for increasing the number or the size of the model (the penalty enforces parsimony in the number of parameters). According to Table 3 and the AIC, the model with a different log σ_i for each moraine is the best one among our three investigated models.

Table 3

Charquini south glacier: Comparison among different GEV models defined by Equation 5. Four models for the log-scale shape parameter log σ_i are compared in this table. The location µ_i parameter is represented as a linear function, and the shape parameter ξ_i is assumed to be a constant.

Moraine Ages Estimates

Table 4 provides the estimated ages and their 95% associated confidence intervals for model 1 in Table 3. As a supplement of Table 4, Figure 4 displays the estimated ages in function of the estimated location parameter µ (see the horizontal lines). The width of these horizontal segments shows the 95% confidence interval length of the estimated ages. The vertical lines represent the range of the dated surfaces. Again, we would like to stress that these 95% intervals are not comparable to the ones obtained with past lichenometric approaches. These past methods were based on the false assumption of a Gaussian distribution despite the fact that probability theory and practice (see Fig. 1) dictate that the shape of the GEV distribution is more appropriate.

Table 4

Estimated ages, Charquini south glacier.

Figure 4

A new type of growth curve plot. The horizontal lines correspond to the estimated location parameters µ of the GEV distribution [see Equations (1) and (2)] for each of the 10 moraines. The width of these horizontal segments shows the 95% confidence interval length of the estimated ages. The vertical lines represent the range of the dated surfaces.

Conclusions and Future Work

Besides the small size of the computed errors in Figure 4, the main improvement over past methods is that the proposed model is more general and more theoretically sound. Still, a number of important statistical questions remains in lichenometry. The model we proposed here only works for block maxima. However, it may be more statistically robust to sample not only the largest size per block but the second or third largest lichens. Determining a mathematical criterion for choosing the most appropriate sampling scheme remains a fundamental question in lichenometry. We believe that extreme value theory can be a valuable tool to perform such a task. Another interesting challenge is determining how to pool data coming from glaciers in the same vicinity. For example, one can imagine that a large quantity of lichen diameters are measured on moraines located on a glacier near the Charquini glacier. If these two glaciers are geographically close, they should share a range of similar characteristics and this could improve the error analysis. In the near future, we plan to investigate these two issues.

Due to the theoretical origin of the GEV distribution, it is difficult to dispute our modeling of maximum diameters; however, it is important to recognize that our proposed global model and estimation strategy are not unique. One may prefer to construct a different link between dates and diameters. For example, a Bayesian approach could also be implemented or a hidden Markov model could used to model this relationship. Our objective in this paper was to show that a “simple” parametric model could perform reasonably well for fitting our data set, but other levels of complexity (if some of our assumptions are not true or more information is available) could be added and lead to a slightly different error analysis.

Finally, we are currently working on making available to the lichenometry community a user-friendly program on the web that will allow the practitioner to test our approach with their own data.